Our goals
For the long term goal of PhoenixD, we aims to form an integrated platform for optical simulations, data sharing across experimental and theoretical groups, and data management following European protocols to allow model, algorithm and data re-usability. OPTISIM is heading for collaborative work on an interface platform to support the long-term vision of PhoenixD.
The platform will be oriented towards the need for research and development within PhoenixD and some part also to our community globally. It will explain and show the models, theory, function, structure and interfaces of different modules in a systematic way. OPTISIM aims to integrate the in-house code, commercial software interface (licenses within the PhoenixD) and other open-source algorithms for computational photonics and optics into one framework.
Though this is an ambitious and long term task, our first stage of OPTISIM is to define the framework. Such platform needs to be established and developed for long term requirements in research and training. OPTISIM will be developed by following systematic software engineering best practices for maintainability, user-friendliness, expandability, and portability on different computing platforms (from desktop computer to exascale supercomputers). The structure of OPTISIM will support the integration of new modules. Proper data structures will be defined to allow exchange of data between modules. This software would represent a foundation for a virtual lab for the OPTICUM (new infrastructure building in campus Garbsen) to simulate complex optical problems, including multiphysics and multiscale scenarios, as well as for the design and optimization of advanced photonic devices.
Our research topics
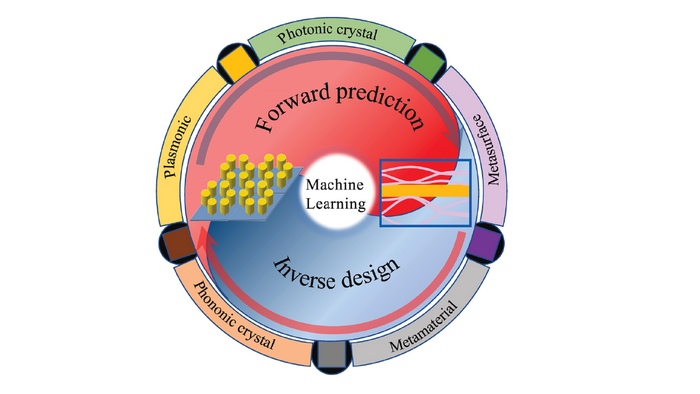
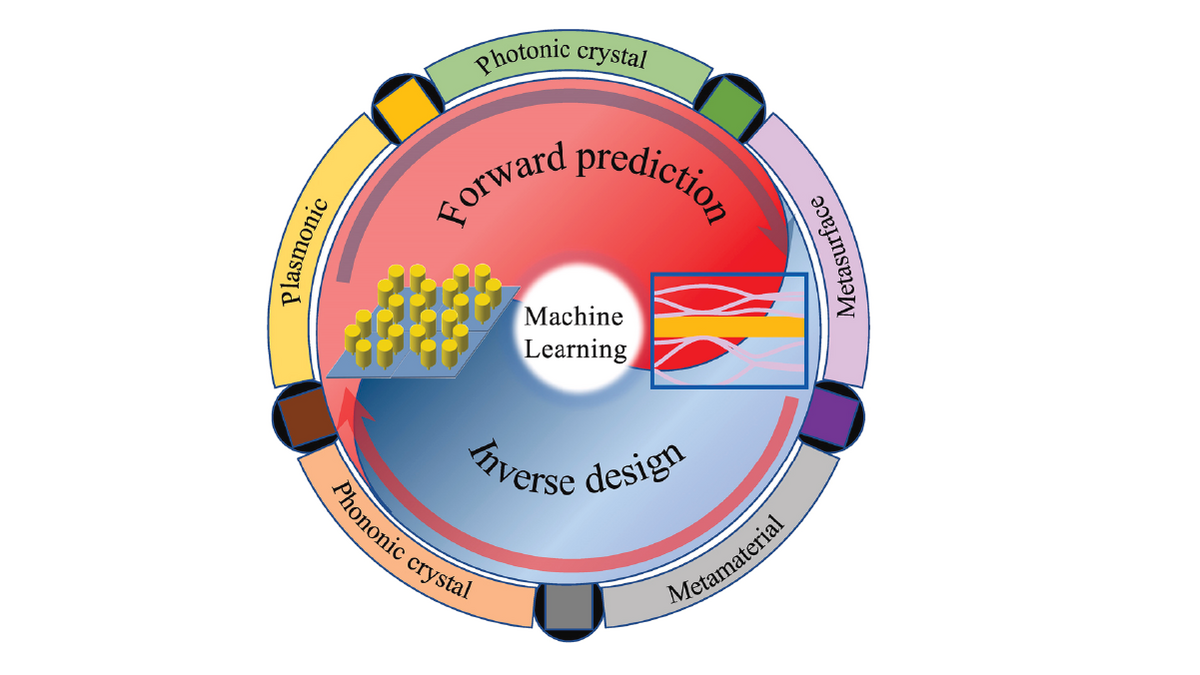
Multiscale modeling and AI
Area manager: Prof. Xiaoying Zhuang
Machine learning and computational mechanics for the modelling and design of novel photonic systems, metamaterials and nanostructures.
-
Example: Promising Photocatalysis in Two-dimension Confirmed by First-principles
![]()
![]()
![]()
Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles.
For the firsttime we show that machine learning interatomic potentials trained over small supercells canbe employed to examine the flexoelectric and piezoelectric properties of complex structures.As the most exciting finding, WSi2N4, CrSi2N4 and MoSi2N4 are found to exhibit the highestpiezoelectric coefficients, outperforming all other-known 2D materials. Our results highlightthat MA2Z4 nanosheets not only undoubtedly outperform the transition metal dichalcogenidesgroup but also can compete with graphene in many applications in nanoelectronics,optoelectronic, energy storage/conversion and thermal management systems.
The original publication is available at https://doi.org/10.1016/j.nanoen.2020.105716
The work is done by the team Prof. Xiaoying Zhuang.
Reference
- K.S. Novoselov, A.K. Geim, S. V Morozov, D. Jiang, Y. Zhang, S. V Dubonos, I. V Grigorieva, A.A. Firsov, Electric field effect in atomically thin carbon films., Science. 306 (2004) 666–9.
- A.K. Geim, K.S. Novoselov, The rise of graphene, Nat. Mater. 6 (2007) 183–191.
- K.S. Novoselov, A.K. Geim, S. V Morozov, D. Jiang, Y. Zhang, S. V Dubonos, I. V Grigorieva, A.A. Firsov, Electric field effect in atomically thin carbon films., Science. 306 (2004) 666–9.
-
Open-Scource Code: A nonlocal operator method for waveguide problem
![]()
![]()
![]()
A novel nonlocal operator theory based on the variational principle is proposed for the solution of partial differential equations. Common differential operators as well as the variational forms are defined within the context of nonlocal operators. The present nonlocal formulation allows the assembling of the tangent stiffness matrix with ease and simplicity, which is necessary for the eigenvalue analysis such as the waveguide problem. The present formulation is applied to solve the differential electromagnetic vector wave equations based on electric fields. The governing equations are converted into nonlocal integral form. An hourglass energy functional is introduced for the elimination of zero- energy modes. Finally, the proposed method is validated by testing three classical benchmark problems.
The original publication is available at https://doi.org/10.32604/cmc.2019.04567
The work is done by the team Prof. Xiaoying Zhuang durchgeführt.
Reference
- Kamensky, David, et al. Immersogeometric cardiovascular fluid–structure interaction analysis with divergence-conforming B-splines. Computer methods in applied mechanics and engineering 314 (2017): 408-472.
- Ren, Huilong, Xiaoying Zhuang, and Timon Rabczuk. Dual-horizon peridynamics: A stable solution to varying horizons. Computer Methods in Applied Mechanics and Engineering 318 (2017): 762-782.
- Kamensky, David, et al. Immersogeometric cardiovascular fluid–structure interaction analysis with divergence-conforming B-splines. Computer methods in applied mechanics and engineering 314 (2017): 408-472.
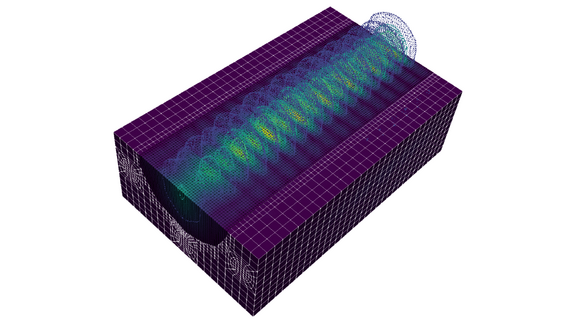
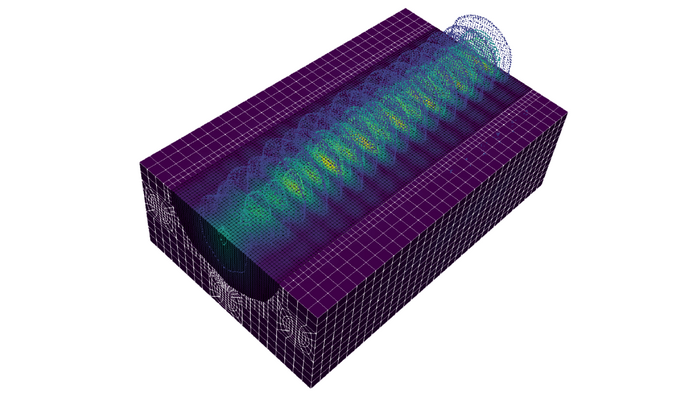
Scientific computing of nonlinear coupled problems in optics
Area manager: Prof. Thomas Wick
Mathematical modeling, adaptive discretizations, and efficient numerical nonlinear and linear solutions of novel problems in optical systems.
-
Open-Source-Code: Parallel domain decomposition solvers for the time harmonic Maxwell equations
![]()
![]()
![]()
The time harmonic Maxwell (THM) equations are of great interest in applied math- ematics and current physics applications, e.g., the excellence cluster PhoenixD. However, the numerical solution is challenging. This is specif- ically true for high wave numbers. Various solvers and preconditioners have been proposed, while the most promising are based on domain decomposition methods (DDM).
The goal of this work is to employ a domain decomposition method and to re-implement the algorithm in the modern finite element library deal.II. Therein, the construction of the subdomain interface conditions is a crucial aspect for which we use Impedance Boundary Conditions. Instead of handling the resulting linear system with a direct solver, which is typically done for the THM, we apply a well chosen block preconditioner to the linear system so we can solve it with an iterative solver like GMRES (generalized minimal residuals). Additionally high polynomial Nédélec elements are used in the implementation of the DDM. This implementation is computationally compared to several other (classical) preconditioners such as incomplete LU, additive Schwarz, Schur complement. These comparisons are done for different wave numbers. Higher wave numbers are well- known to cause challenges for numerical solution.
The original publication is available at https://link.springer.com/chapter/10.1007/978-3-030-95025-5_71
Read more and download the code from here: https://github.com/tommeswick ; https://github.com/kinnewig
The work is done by S. Beuchler, S. Kinnewig, and T. Wick within the team led by Prof. Thomas Wick.
-
Open-Scource Code: Algorithmic realization of the solution to the sign conflict problem for hanging nodes on hp-hexahedral Nédélec elements
![]()
![]()
![]()
While working with Nédélec elements on adaptively refined meshes with hanging nodes, the orientation of the hanging edges and faces must be taken into account. Indeed, for non-orientable meshes, there was no solution and implementation available to date. The problem statement and corresponding algorithms are described in great detail. As a model problem, the time-harmonic Maxwell's equations are adopted because Nédélec elements constitute their natural discretization. The implementation is performed within the finite element library deal.II. The algorithms and implementation are demonstrated through four numerical examples on different uniformly and adaptively refined meshes.
The original publication is available at https://arxiv.org/abs/2306.01416
Read more and download the code from here: https://github.com/tommeswick, https://github.com/kinnewig
The work is done by S. Kinnewig, T. Wick, S. Beuchler within the team led by Prof. Thomas Wick.
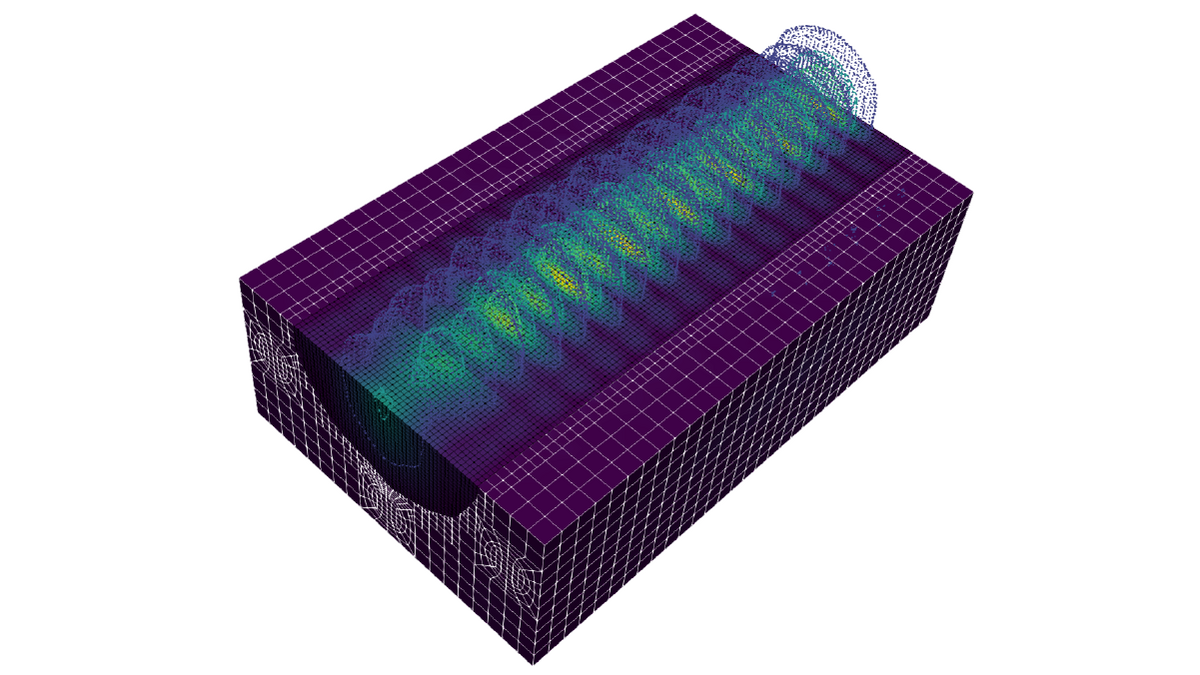
Computational Nonlinear Optics
Area manager: Prof. Ayhan Demircan
Theoretical and computational investigations of multi-physics and multi-scale problems in nonlinear optical systems.
-
Open-Source Code: A generalized nonlinear Schrödinger Python module implementing different models of input pulse quantum noise
![]()
![]()
![]()
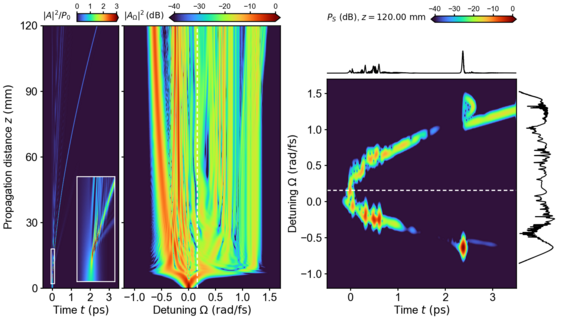
We provide Python tools enabling numerical simulation and analysis of the propagation dynamics of ultrashort laser pulses in nonlinear waveguides. The modeling approach is based on the widely used generalized nonlinear Schrödinger equation for the pulse envelope. The provided software implements the effects of linear dispersion, pulse self-steepening, and the Raman effect. The focus lies on the implementation of input pulse shot noise, i.e. classical background fields that mimic quantum noise, which are often not thoroughly presented in the scientific literature. We discuss and implement commonly adopted quantum noise models based on pure spectral phase noise, as well as Gaussian noise. Coherence properties of the resulting spectra can be calculated. We demonstrate the functionality of the software by reproducing results for a supercontinuum generation process in a photonic crystal fiber, documented in the scientific literature. The presented Python tools are open-source and released under the MIT license in a publicly available software repository.
Platform: Python, using the functionality of numpy, scipy and matplotlib.
Read more and download the code from here:
https://github.com/ElsevierSoftwareX/SOFTX-D-22-00165.gitWe prepared a Code Ocean capsule, allowing to directly run and modify an exemplary simulation without the need to create a local copy of the repository under the link:
https://codeocean.com/capsule/4658074/treeThe work is done by the team of Prof. Ayhan Demircan
Reference
- Melchert, Oliver and Demircan, Ayhan. GNLStools.py: A generalized nonlinear Schrödinger Python module implementing different models of input pulse quantum noise. SoftwareX 20 (2022): 101232.
- Melchert, Oliver et al. Soliton compression and supercontinuum spectra in nonlinear diamond photonics. Diamond & Related Materials 136 (2023): 109939.
- Melchert, Oliver and Demircan, Ayhan. GNLStools.py: A generalized nonlinear Schrödinger Python module implementing different models of input pulse quantum noise. SoftwareX 20 (2022): 101232.
-
Open-Scource Code: A python package for ultrashort optical pulse propagation in terms of forward models for the analytic signal
![]()
![]()
![]()
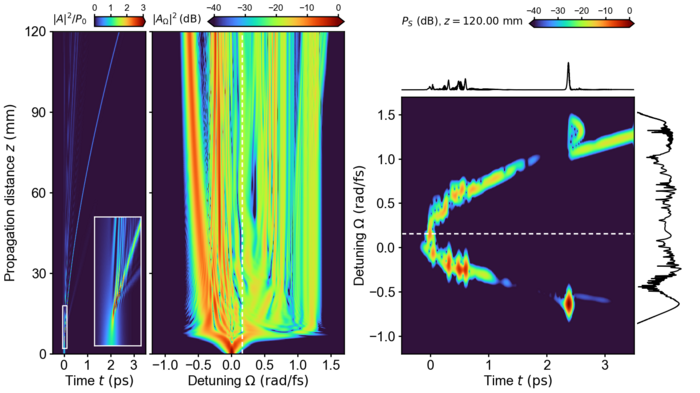
We present a flexible, open-source Python package for the accurate simulation of the z-propagation dynamics of ultrashort optical pulses in nonlinear waveguides, especially valid for few-cycle pulses and their interaction. The simulation approach is based on unidirectional propagation equations for the analytic signal. The provided software allows to account for dispersion, attenuation, four-wave mixing processes including, e.g., third-harmonic generation, and features various models for the Raman response. The propagation equations are solved on a periodic temporal domain. For z-propagation, a selection of pseudospectral methods is available. Propagation scenarios for a custom propagation constant and initial field pulses can either be specified in terms of a HDF5 based input file format or by direct implementation using a python script. We demonstrate the functionality for a test-case for which an exact solution is available, by reproducing exemplary results documented in the scientific literature, and a complex propagation scenario involving multiple pulses.
Platform: Python, using the functionality of numpy, scipy and matplotlib.
Read more and download the code from here: https://data.mendeley.com/datasets/7s2cv9kjfs/1
We prepared a Code Ocean capsule, allowing to directly run and modify an exemplary simulation without the need to create a local copy of the repository under the link: https://codeocean.com/capsule/4971866/tree
The work is done by the team of Prof. Ayhan Demircan.
Reference
-
Melchert, Oliver and Demircan, Ayhan. py-fmas: A python package for ultrashort optical pulse propagation in terms of forward models for the analytic signal. Computer Physics Communications 273(2022): 108257.
-
Melchert, Oliver et al. Resonant Kushi-comb-like multi-frequency radiation of oscillating two-color soliton molecules. New J. Phys. 25 (2023): 013003.
-
Melchert, Oliver et al. (Invited) Two-color soliton meta-atoms and molecules. Optik 280 (2023): 170772.
-
Melchert, Oliver and Demircan, Ayhan. Two-color pulse compounds in waveguides with a zero-nonlinearity point. Opt. Lett. 48 (2023): 518.
-
-
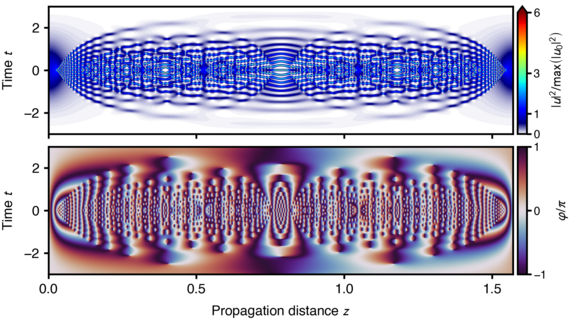
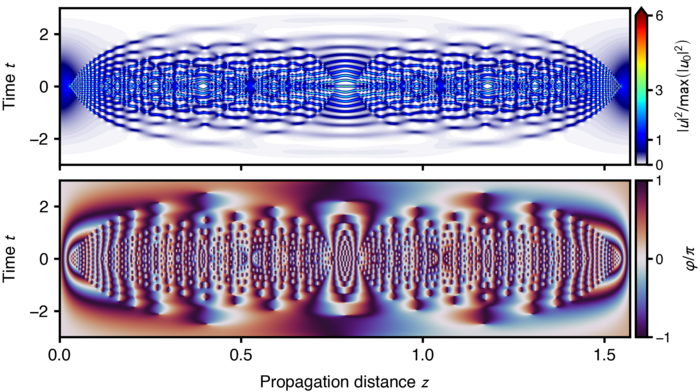
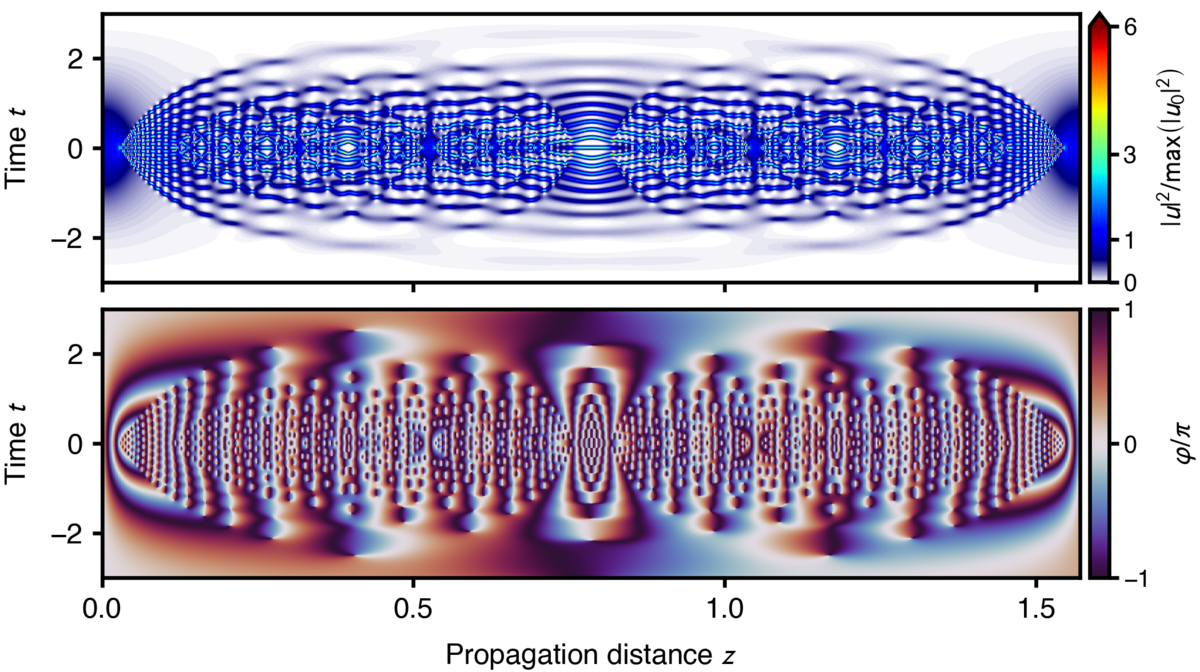
Open-Scource Code: A Python toolkit for solving the generalized Lugiato–Lefever equation
![]()
![]()
![]()
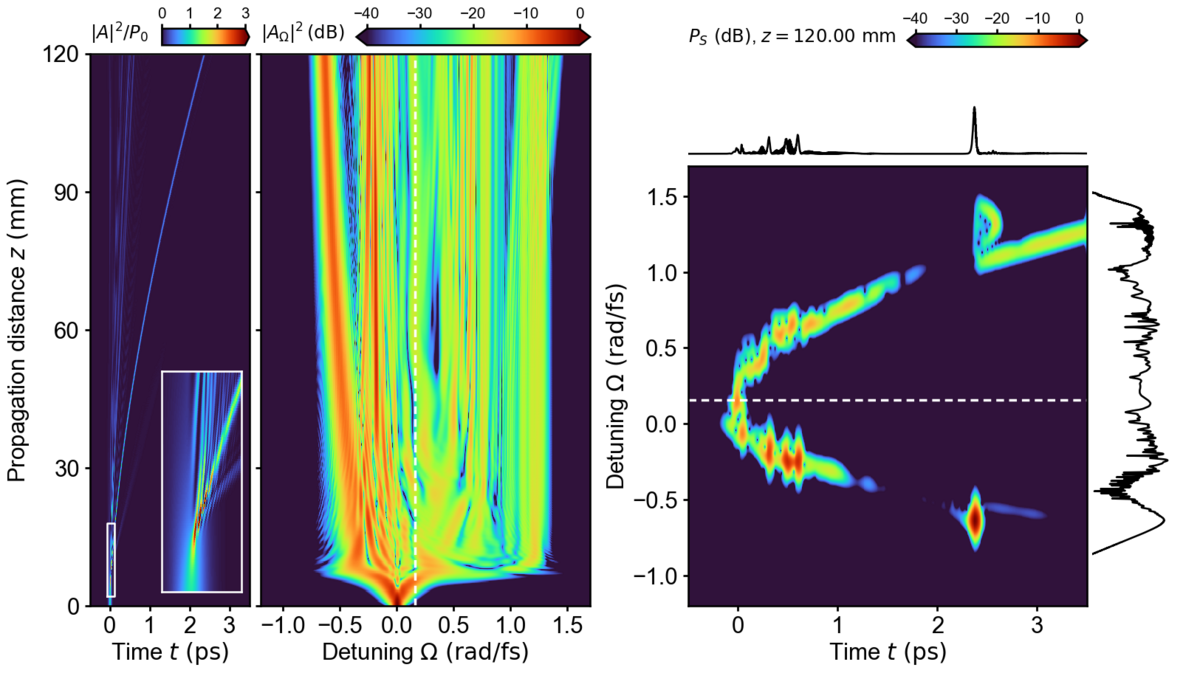
We present a Python toolkit for simulating the propagation dynamics of dissipative solitons in a variant of the Lugiato–Lefever equation (LLE) including dispersion terms of third and fourth order. In addition, the provided software allows to prepare initial conditions given by stationary localized solutions of the standard LLE in the anomalous group-velocity dispersion regime. Propagation scenarios for custom control parameters and initial conditions can be specified by the user via a simple class data structure. We demonstrate the implemented functionality by showing how to obtain stationary solutions of the standard LLE containing a dissipative soliton, and, demonstrating different characteristic propagation scenarios. The pyGLLE software package is open-source and released under the X11 License in a publicly available software repository.
Platform: Python, using the functionality of numpy, scipy and matplotlib.
Read more and download the code from here: https://github.com/ElsevierSoftwareX/SOFTX_2020_88.git
We prepared a Code Ocean capsule, allowing to directly run and modify an exemplary simulation without the need to create a local copy of the repository under the link: https://codeocean.com/capsule/9315811/tree
The work is done by the team of Prof. Ayhan Demircan.
Reference
-
Melchert, Oliver and Demircan, Ayhan. pyGLLE: A Python toolkit for solving the generalized Lugiato–Lefever equation. SoftwareX 15 (2021): 100741.
-
Melchert, Oliver and Demircan, Ayhan and Yulin, Alexey. Multi-frequency radiation of dissipative solitons in optical fiber cavities. Scientific Reports 10 (2020): 8849.
-
Melchert, Oliver and Yulin, Alexey and Demircan, Ayhan. Dynamics of localized dissipative structures in a generalized Lugiato–Lefever model with negative quartic group-velocity dispersion. Opt. Lett. 45 (2020): 2764.
-
-
Open-Scource Code: Analytic signal spectrograms with optimized time–frequency resolution
![]()
![]()
![]()
A Python package for the calculation of spectrograms with optimized time and frequency resolution for application in the analysis of numerical simulations on ultrashort pulse propagation is presented. Gabor’s uncertainty principle prevents both resolutions from being optimal simultaneously for a given window function employed in the underlying short-time Fourier analysis. Our aim is to yield a time– frequency representation of the input signal with marginals that represent the original intensities per unit time and frequency similarly well. As a use-case, we demonstrate the implemented functionality for the analysis of simulations on ultrashort pulse propagation in a nonlinear waveguide.
Platform: Python, using the functionality of numpy, scipy and matplotlib.
Read more and download the code from here: https://github.com/ElsevierSoftwareX/SOFTX_2019_130
We prepared a Code Ocean capsule, allowing to directly run and modify an exemplary simulation without the need to create a local copy of the repository under the link: https://codeocean.com/capsule/7823161/tree
The work is done by the team of Prof. Ayhan Demircan.
Reference
Melchert, Oliver and Roth, Bernhard and Morgner, Uwe and Demircan, Ayhan. OptFROG — Analytic signal spectrograms with optimized time–frequency resolution. SoftwareX 10 (2019): 100275.
Our competences
Research area - Multiscale modeling and AI
Prof. Xiaoying Zhuang’s key research area is machine learning and computational mechanics for the modelling and design of novel photonic systems, metamaterials and nanostructures. She has developed numerous innovative and robust numerical methods including level-set methods, partition-of-unity methods (such as mesh-free methods, XFEM formulations, phantom node methods and finite cover methods), multiscale methods, phase field models and error-driven adaptive methods developed and implemented. She also has experience with coupled (hydro-mechanical, thermo-mechanical, thermo-hydro-mechanical and electro-mechanical) problems, uncertainty analyzes/uncertainty quantification as well as inverse methods and optimization processes. She has applied innovative numerical methods to solve complex problems in engineering, solid state physics, and materials science. The research focus of Sofja Kovalevskaja Project funded by the Humboldt Foundation is the modeling, optimization and development of polymer composite materials. Her ongoing ERC Starting Grant is focused on the optimization and development of piezoelectric and flexoelectric nano-energy converters.
Research area - Computational Nonlinear Optics
The group's research activities is concerned with theoretical investigation of complex dynamics appearing in nonlinear systems in different fields. These fields include modern nonlinear optics, quantum optics, material science and condensed matter physics, but also fluid dynamics and related fields. The investigations comprise theoretical analyses of the fundamental effects, modelling, as well as developing and applying adequate numerical methods. A wide range of methods varying from spectral and statistical methods to finite difference time domain schemes are developed and applied. Our activities can be divided into three main categories: method development, nonlinear wave interaction and soliton physics, and nonlinear condensed matter photonics.
Research area-Scientific computing of nonlinear coupled problems in optics
Prof. Thomas Wick's research interests are design, implementation and analysis of numerical algorithms and space-time methods for nonstationary, nonlinear, coupled PDE systems and variational inequalities within the fields for computational fluid dynamics, solid mechanics, fluid-structure interaction, thermoporoelasticity, and crack propagation problems in elasticity and poroelasticity. Therein he is specifically interested nonlinear solvers, a posteriori error estimation, adaptive methods such as local mesh adaptivity with a particular emphasis on goal-oriented techniques using adjoints, and parallel high performance computing. These concepts are furthermore employed in numerical optimization for optimal control, optimal design and parameter estimation. An important part of Prof. Wick's group work is concerned with sustainable, modern, research software developments.